Классификация изомерии по виду операций

№ п.п. Изомерия (симметрия)	№ п. п. Изомерия (симметрия)	№ п.п Изомерия (симметрия)
1 классическая	19 конформная	37 проективная
2. анти-	20 конф. анти-	38 пр. анти-
3 кр. анти-	21 конф. кр. анти-	39 пр. кр. анти-
4 цв.	22 конф. цв.	40 пр. цв.
5. цв. анти-	23 конф. цв. анти-	41 пр. цв. анти-
6. цв. кр. анти-	24 конф. цв. кр. анти-	42 пр. цв. кр. анти-
7. кр. цв.	25 конф. кр. цв.	43 пр. кр. цв.
8. кр. цв. кр. анти-	26 конф. кр. цв. кр. анти-	44 пр. кр. цв. кр. анти-
9. крипто-	27 конф. крипто-	45 пр. крипто-
10. подобия	28 аффинная	46 топологическая
11. под. анти-	29 афф. анти-	47 топ. анти-
12. под. кр. анти-	30 афф. кр. анти-	48 топ. кр. анти-
13. под. цв.	31 афф. цв.	49 топ. цв.
14. под. цв. анти-	32 афф. цв. анти-	50 топ. цв. анти-
15. под. цв. кр. анти-	33 афф. цв. кр. анти-	51 топ. цв. кр. анти-
16. под. кр. цв.	34 афф. кр. цв.	52 топ. кр. цв.
17. под. кр. цв. кр. анти-	35 афф. кр. цв. кр. анти-	53 топ. кр. цв. кр. анти-
18. под. крипто-	36 афф. крипто-	54 топ. крипто-

Классификация изомерии по виду операций, посредством которых одна изомерная структура переходит в другую изомерную структуру, позволила вывести 54 структурные изомерии, из которых 53 оказались существенно новыми. Это крипто-, простые и кратные анти- и (или) цветные классическая, подобия, конформная, аффинная, проективная, топологическая изомерии (см. табл. 6).
В настоящее время закончено построение моделей каждой из 54 изомерий, кроме того, установлена возможность удвоения, утроения и т. д. числа структурных изомерий за счет изменения закона комбинирования качеств ( + , ; цветных, крипто-) как друг с другом, так и с основными геометрическими преобразованиями (евклидовыми, подобия, конформными и т.д.).
Изучение с точки зрения ОТС даже известной стереохимикам оптической, или, строже, диссимметрической изомерии, помогло нам [94] доказать существование трех типов диссизомерий: I типа (старого), число изомеров S для которого Sk° k° = 2 k° (изомерия альдогексоз и листьев липы); II типа (нового), S для которого

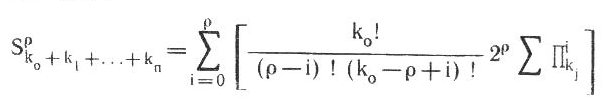
(его примеры изомерия пираногексоз и изолированных корней некоторых растений); III типа (также нового), S для которого S1o+k1 =2k1 (изомерия пираногексоз с k0 = 0 и циклических венчиков с нечетным числом взаимно перекрывающихся лепестков).
Проанализируем теперь связь учения об изомерии с теорией групп и симметрии, центральным предложением ОТС и проблемой «состав строение свойство». Тем самым мы продолжим построение общей теории изомерии.

Изомерия и симметрия. Связь изомерии с симметрией доказывается посредством теории групп подстановок. Дело в том, что эту теорию и вообще математическое учение о перестановках содержательно можно интерпретировать как учение об изомерии.

В самом деле, с точки зрения математики изомер это перестановка, изомерия множество перестановок, изомеризация это подстановка, верхняя строка которой означает предмет, а нижняя результат изомеризации; следующие друг за другом изомеризации есть произведение подстановок. Совокупность всех подстановок для действия умножения подстановок образует группу подстановок. Следовательно, совокупность всех изомеризации для действия «умножения» изомеризации также образует группу группу изомерии, а следовательно, выявляет и определенного рода изомерийную симметрию, которая предстает как сохранение состава изомеров при изомеризациях. Благодаря этим операциям одни изомеры данной совокупности переходят в другие изомеры той же совокупности, а вся совокупность по составу «первичных» элементов и составу изомеров «совмещается сама с собой».

Сказанное позволяет сформулировать следующее предложение.
Предложение 11. Всякая конечная группа всех изомеризации n-й степени группа In изоморфна группе всех подстановок n-й степени группе Sn.
Математический изоморфизм теории групп подстановок теории групп изомерии позволяет автоматически переносить знания из первой области во вторую. В частности, имеет место следующее.
Теорема Кэли. Всякая конечная группа порядка n изоморфна некоторой подгруппе группы всех подстановок n-й степени. Следующее предложение ее изомерийный аналог.
Предложение 12. Всякая конечная группа порядка n изоморфна некоторой подгруппе группы всех изомеризации n-й степени. Отсюда сразу получаем предложение 13.

Предложение 13. Всякая конечная группа симметрии порядка n изоморфна некоторой подгруппе группы всех изомеризации n-й степени.
Изоморфизм симметрии и изомерии, установленный здесь по крайней мере для их конечных групп, позволяет благодаря возможности переноса знаний из одной области в другую по меньшей мере, во-первых, считать список 64 фундаментальных и 54 структурных изомерии списком также 64 фундаментальных и 54 структурных симметрий. Сказанное объясняет, почему упомянутые таблицы 5 и 6 есть таблицы также симметрии известных и впервые найденных; во-вторых, ввести представления о непрерывных и дискретных преобразованиях изомерии, конечных и бесконечных группах изомерии; в-третьих, ввести представление о размерности изомерии.
Будем считать изомерию n-мерной (n = 0, 1, 2, 3), если каждый изомер данной совокупности обладает n-мерной симметрией точечной, линейной, плоской, пространственной. Например, изомерия асимметричных альдогексоз состава С6Н12О6 или асимметричных листьев липы 0-мерная, потому что каждому из 16 изомеров соответственно альдогексозы и листа липы присуща точечная группа симметрии (1). Изомерия побегов растений с левым или правым листорасположением одномерная, потому что каждому изомеру побега присуща одномерная, или линейная, симметрия, описываемая одной из групп симметрии «стержней».

Однако нередко при изомеризациях симметрия изомера меняется. Например, в зависимости от ионной силы и температуры раствора молекулы РНК могут существовать то в виде «клубков», обладающих точечной симметрией, то в виде «нитей», обладающих одномерной симметрией. Соответственно и изомерия таких объектов будет не n-мерная, a n1 n2 ... nk -мерная.

В приведенном примере она 01-мерная.
В-четвертых, появляется возможность предложить новую идею о возможности развития теории групп n1 n2 ... nk -мерной симметрии, в которой размерность объекта при преобразованиях симметрии уже не оставалась бы инвариантной.
В-пятых, это позволяет сделать новый для классической теории структурной симметрии вывод о возможности реализации любого диссимметрического (правого или левого) или недиссимметрического объекта соответственно в виде не двух или одного, а двух или большего (в пределе бесконечного) числа модификаций. Данный вывод прямо следует, например, из возможности существования любого диссимметрического или недиссимметри-ческого изомера в виде двух или большего числа изомерных, а шире полиморфических модификаций. Тот же вывод следует из развитой нами теории диссфакторов [91; 94].
Изомерия и центральное предложение ОТС. Казалось бы, изомерия может быть порождена только благодаря относительному преобразованию. Однако в статье «О значении основных законов преобразования объектов-систем для биологии» мы писали «о возможности возникновения изомерии от исходных объектов всеми семью способами» [98.

С. 132]. В табл. 7 приведены «лингвистические», разумеется сугубо условные, модели всех семи способов порождения изомерии.

Из таблицы видно, что вопреки широко распространенным представлениям изомерия может возникнуть посредством, казалось бы, и неизомеризационных способов.
Таблица 7. Лингвистические модели порождения изомерии множества {сон, нос} семью способами

№	Способ	Модель
	Количественный	сонный ------ (- «ный»)------- сон ноский -------( - «кий») ------ нос
	Качественный	кон --------- ( к-с ) -------- сон нож ---------- ( ж -с) -------- нос
	Относительный	нсо -------------------------------------- нос нсо --------------------------------------- сон
	Колич + Кач	соринка --- (-«инка») сор --- р-н -- сон тоска --------(-«ка») --- тос ---т-н -- нос
	Колич + Относ	носки ---- (- «ки») --- нос ----------- сон сновидение (- «видение») -- сно -- нос
	Кач + Относ	дом --- (д -с)(м -с) ---нос ------- сон сор --------( р -н ) ---------сон ------- нос
	Колич + Кач + Относ	домкрат (-«крат») дом (д- н)(м- с) нос сон соратник --(-«атник»)-- сор--- (р -н )-- сон -- нос

Столь же неверным является и другое традиционное мнение, будто сугубо изомеризационное относительное преобразование всегда приводит к возникновению изомерии. В действительности такое преобразование может приводить к превращению изомерной совокупности в изомерную же (например, множества {сон, нос} во множество {нсо, сно}), неизомерной в неизомерную (например, множества {сон} во множество {нос}), неизомерной в изомерную и наоборот (например, множества {сон} во множество {нос, нсо} или множества {нос, нсо} во множество {сон}).
Неправильным оказывается и третье традиционное представление о том, что лишь при относительном преобразовании состав изменяемых объектов не изменяется.

Содержание раздела