Закон действительно существует
подавляющее большинство) фактически совпадают с представлением о системе как особом «единстве», «целостности», «целостном единстве». Таковы определения Л. Берталанфи, К. Черри, Дж. Клира, А. Раппопорта, В. И. Вернадского, О. Ланге, П. К. Анохина, Л. А. Блюменфельда, И. В. Блауберга, В. Н. Садовского и Э. Г. Юдина.
В сущности все эти определения можно рассматривать как весьма приблизительные определения «объекта-системы». Рассмотрим типичный пример. И. В. Блауберг, В. Н. Садовский, Э. Г. Юдин считают, что 1) система представляет собой целостный комплекс взаимосвязанных элементов; 2) она образует особое единство со средой; 3) обычно исследуемая система представляет собой элемент системы более высокого порядка; 4) элементы любой исследуемой системы в свою очередь обычно выступают как системы более низкого порядка [73]. А. И. Уемов справедливо считает, что признаки 3 и 4 «не могут быть включены в определение, поскольку... это не общие признаки всех систем, а лишь «обычно» встречающиеся. Обычно натуральные числа, с которыми мы имеем дело, не очень велики.
Но это не значит, что указанный признак следует включать в общее определение натурального числа» [86].
И все же главный недостаток определений системы как (фактически) особого рода объекта-системы заключается в том, что в этих дефинициях не учитывается существование кроме объектов-систем еще и систем объектов-систем одного и того же рода, что служит основной причиной неполноты всех так называемых целостных дефиниций системы. Докажем это, одновременно продолжив построение ОТС.
3. Вывод и определение понятия «система объектов одного и того же рода». Закон системности. Алгоритм построения системы объектов данного рода
Комбинация (1) (4) (2) (3) «существует единство множества объектов единых» означает и «существует объект-система». Но «существует» значит, покоится или изменяется. Покой объекта-системы можно рассматривать как его непрерывный переход (во времени) в себя, а логически как тождественное преобразование. Впервые это преобразование как системное было эксплицировано А. В. Маликовым.
Изменение же объекта-системы всегда приводит к переходу его по определенным законам в один или большее число других объектов-систем. Последние в свою очередь превращаются в третьи, третьи в четвертые объекты-системы и т. д. Причем если учесть, что движение абсолютно, а покой относителен, то естественно признать такие превращения неизбежными. Возникающие таким способом объекты-системы могут оказаться качественно одинакового или (и) разного рода.
Определение 2. Система объектов данного (i-ro) рода это в сущности закономерное множество объектов-систем одного и того же рода. Причем выражение «одного и того же, или «данного, рода» означает, что каждый объект-система обладает общими, родовыми признаками (одним и тем же качеством), а именно: каждый из них построен из всех или части фиксиро-ианных «первичных» элементов m множества {Мi(0)} в соответствии с частью или со всеми фиксированными отношениями r множества {Ri}, с частью или со всеми фиксированными законами композиции z множества {Zi}, реализованными в рассматриваемой системе объектов данного рода. Как для объекта-системы, так и для системы объектов одного и того же рода множества {Zi}; {Zi} и {Ri}; {Zi}, {Ri} и {Мi(0)} могут быть пустыми или содержать от одного до бесконечного числа элементов.
Весьма наглядным примером системы объектов одного и того же рода являются предельные углеводороды СН4, С2Н6, С3Н8, ..., СS-1H2(S-1)+2, CSH2S+2: все они построены из одних и тех же «первичных» элементов С и Н в соответствии с одним и тем же отношением химического сродства и согласно одному и тому же закону композиции вида СnН2n+2 (n = 1, 2, 3, .... S).
Примерами систем объектов тех или иных родов могут служить и системы точечных, линейных, плоских, пространственных (классических и неклассических) групп симметрии, системы чисел натурального ряда, периодическая система химических элементов Д. И. Менделеева, гомологические ряды в химии и в биологии, периодическая система венчиков и цветков растений, естественные и искусственные системы растений и животных, система общественно-экономических формаций, лингвистическая система из шести слов-изомеров сон, нос, нсо, сно, онс, осн.
Из определения 2 и приведенных примеров следует, что система объектов одного и того же рода это закономерная совокупность в общем случае не входящих друг в друга, отдельно сушествующих объектов-систем, а не один объект, устроенный по типу русских матрешек. Уже это доказывает неполноту определений «системы вообще» только как «объекта-системы вообще» и иерархического объекта-системы в особенности.
Исключительно широкое распространение систем объектов тех или иных родов в природе, обществе, мышлении дает основание полагать, что существует некий закон, сохраняющий свою справедливость для неживой, живой природы и общества. И такой закон действительно существует.
Предложение 2. Закон системности. Любой объект есть объект-система и любой объект-система принадлежит хотя бы одной системе объектов данного рода.
Справедливость этого закона прямо следует из определений 1, 2 и предложения 1. Заметим, что здесь и далее тем или иным предложениям дается статус «закона ОТС» в том случае, если они, отображая существенные, повторяющиеся особенности систем, имеют фундаментальное онтологическое и гносеологическое значение.
Закон системности по охвату реальности один из абсолютных законов ОТС. Его проявления в природе, обществе и мышлении не могли бы быть осознаны без ясного понимания и онтологического статуса ОТС, без отвечающего требованию полноты определения объекта-системы, без открытия существования принципиально нового вида систем систем объектов одних и тех же родов.
С законом системности связаны два алгоритма: алгоритм представления объекта как объекта-системы (см. параграф 2 настоящей главы) и алгоритм построения системы объектов одного и того же рода, к изложению которого мы и переходим.
Алгоритм построения системы объектов данного рода. В самом общем виде данный алгоритм можно свести к четырем основным шагам:
1. К отбору из универсума {U} по единому основанию Аi(0) некоторой совокупности «первичных» элементов {Мi(0)}.
2. К наложению на «первичные» элементы определенных отношений единства Ri(1) и к образованию благодаря этому по закону Zi(1) множества объектов-систем (композиций) {Мi(1)}.
3. К такому изменению композиций множества {Мi(1)} и к такому выводу (согласно отношениям Ri(2), Ri(3), .., Ri(S) и законам композиции Zi(2), Zi(3), .., Zi(S) множеств композиций {Мi(2)}, {Мi(3)}, ..., {Мi(S)}, при которых эти композиции оказываются построенными из части или всех «первичных» элементов одного и того же множества {Мi(0)}.
4. К выводу всех возможных для данных Ai, Ri, Zi объектов-систем множества {Мi}, или системы объектов данного i-го рода Si = {Мi} = {Мi(0), Мi(1), ..., Мi(S)}.
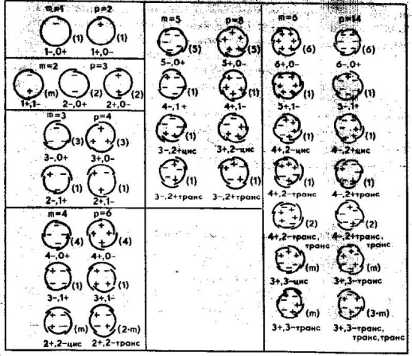
Рис 1. Изомерийно-неизомерийная система циклических венчиков со стыкующимися лепестками (m= 1 6) . Плюсы и минусы при стыках указывают на характер последних; символы в скобках виды симметрии; m число лепестков, Р число изомеров
Пример биологический. Построим систему циклических венчиков со стыкующимися лепестками [см.: 93].
Для этого, согласно шагу 1, по основанию Ал(0) выделим множество первичных элементов {Мл(0)}={л}, содержащее лепестки (индекс «л» лепесток). Согласно шагу 2, наложим на лепестки отношения RB(1) (взаимоналожения по кругу краев одних лепестков на края других) и по закону
ZB(1) =P(m,r) =1/m rk (m/k)
k|m
(m=1) образуем первые два венчика значности: 1+0 и 1 , 0 + , а тем самым и множество {МB(1)}= {1+, 0-; 1-, 0+} из таких венчиков (см. 1).
Согласно шагу 3, изменим композиции множества {МB(1)}, т. е. венчики 1 +, 0 и 1 , 0+ (по отношениям RB(2) = RB(3) = = . ..= RB(S) = RB(1) и закону композиции
ZB(2) = ZB(3) =.. .= P(m, r) = ZB(1) =P(m,r) =1/m rk (m/k)
k|m
таким образом, что образуем все возможные циклические венчики с числом стыкующихся лепестков m = 2, 3, 4, 5, .. ., s; а тем самым и множества {МB(2)}= {1+, 1 ; 2, 0+; 2 + , 0-), {МB(3)}={3+, 0-; 3 , 0+; 2 + , 1 ; 2-, 1 +},..., {МB(S)}=(S + , 0-; S-, 0+; (S-l)+, 1-; (S 1), 1+;…} (см. 1).
Наконец, согласно шагу 4, получим систему циклических венчиков со стыкующимися лепестками SB = {MB}={ МB(0), МB(1), МB(2), ..., МB(S)}, частично схематически изображенную на 1 (m=1 6).
Построение системы объектов данного рода позволяет определить понятие «абстрактная система», или просто «система».
4. Вывод и определение понятия «абстрактная система»
Изучая особенности циклических венчиков со стыкующимися лепестками, мы обнаружили [93], что по таким признакам, как (не) четность числа лепестков т, (не) четность числа значных состояний венчика Z = m+l, изомерия I, симметрия S, система является периодической, ибо с переходом из одной ее клетки в другую все эти признаки изменяются периодически. Далее мы установили, что свойства изомерных совокупностей по ходу системы изменяются по следующему закону: четность, изомерия, симметрия изомерийных совокупностей циклических венчиков находятся в периодической зависимости от числа лепестков т, совпадающего с номером клетки в системе.
- Основной закон ОТС
- Теория групп неэволюционных, эволюционных системных преобразований
- Фрагмент таблицы Кэли группы системных антипреобразований
- Диалектика эволюционных системных преобразований
- Третий закон преобразования композиций системы.
