Какова ваша внутренняя история?
Какова ваша внутренняя история?
Слово - это отнюдь не прозрачный и неизменный кристалл.
Слово - это оболочка живой мысли.
Оно может менять окраску и содержание в зависимости от обстоятельств использования.
Оливер Уэнделл Холмс, юрист
Сила ума. Решение проблем
Все решает время
Вы потерпели кораблекрушение и попали в плен к племени каннибалов.
Вам в руки дают пару песочных часов.
Одни отсчитывают ровно четыре минуты.
Другие - ровно семь.
Вождь требует, чтобы вы сказали, когда пройдет точно девять минут.
Если вы это сделаете, вас освободят.
Если вы не сделаете этого, вас съедят.
Вождь орет: “Начинай немедленно!”
Что делать?
Внутренние побуждения
Жить - значит иметь проблемы. Решать их - значит расти интеллектуально.
Дж. П. Гилдфорд, психолог
Ну и как вы справились с задачей о песочных часах и каннибалах? Когда один мой хороший приятель задал мне эту загадку, он будто бы всунул мне в руки воображаемые часы. Я сел и задумался. Через пару минут приятель сказал: “Все, слишком поздно. Ты упустил свой шанс.
Теперь ты пойдешь на жаркое”. Я возмутился: “Что ты имеешь в виду? Я же еще не сказал, что собираюсь сделать”. - “В том-то и дело! - воскликнул приятель. - Ты просто держал часы в руках, даже не пытаясь их перевернуть.
Поскольку ты ничего не делал, ты опоздал. Даже если ты сумеешь дать правильный ответ, как отмерить девять минут, все равно не выполнишь в точности приказание вождя. Ведь он выкрикнул: “Начинай немедленно!”
Сначала у меня появилось чувство, что меня надули. Но потом я сообразил, что получил хороший урок. Я понял, что не отреагировал на поставленную задачу должным образом - так, как если бы она встала передо мной реально. Я не сумел поставить себя в положение человека, попавшего к людоедам.
Я пытался решить задачу как бы извне.
Так как же вы должны были решать эту задачу, если бы действительно потерпели кораблекрушение? Во-первых, нужно немедленно перевернуть песочные часы! А пока песок сыплется, можно и подумать.
Что происходит дальше? Через четыре минуты первые песочные часы иссякнут, и вы, естественно, снова перевернете их. Через семь минут иссякнут вторые часы.
Переверните их тоже. Еще через минуту (всего через восемь минут) вновь иссякнут первые часы. Поскольку у вас в запасе осталась только одна минута, а на дне вторых часов насыпалось песка тоже ровно на минуту, вы можете быстро их перевернуть.
Когда песок во вторых часах полностью пересыплется, с начала испытания как раз и пройдет девять минут.
Для того чтобы успешно решать практические задачи, необходимо развить базовый набор навыков, которые вы сможете применять практически во всех случаях жизни, при решении проблем - абстрактных, межличностных, денежных, возникающих на работе. К этим навыкам относятся:
- ПРЯМОЙ ПОДХОД. Если перед вами встает проблема, что вы обычно делаете? Идете ей навстречу или бежите от нее? Удовлетворяетесь единственным решением или пытаетесь найти еще и альтернативные? Откладываете решение в долгий ящик или всегда решаете проблему сразу же?
- ОРГАНИЗАЦИЯ. Для того чтобы эффективно решить задачу, нужно правильно организовать имеющуюся информацию, сосредоточиться на ключевых моментах, отбрасывая все второстепенное. Нужно точно сформулировать возникшую проблему. Эйнштейн понимал значение ясности, он говорил: “Все нужно делать так просто, как только возможно, но не более того”.
- МАНИПУЛЯЦИИ. Некоторые задачи решаются достаточно эффективно с помощью продуманной тактики последовательных шагов. Другие можно решить экспериментальным путем - методом проб и ошибок. Третьи сдаются только после долгого размышления, причем ответ часто возникает как озарение. В любом случае вы должны будете оперировать имеющейся в наличии информацией. Возможно, вам придется переставлять слова, рассматривать иллюстрации, разбираться в математических формулах. А возможно, вам придется анализировать свои собственные реакции.
- ПРОВЕРКА. Когда вы получите решение, проверьте его правильность. Вновь проанализируйте сделанные вами допущения, цепочки умозаключений. Спросите себя, нет ли у этой проблемы другого решения.
Поскольку разные типы задач требуют разных типов мышления, не существует универсальной формулы, которая позволяла бы с гарантией решать любые проблемы. В следующем разделе приводятся некоторые задачи, ставшие уже классическими. Вы увидите, что во многих случаях решение содержит элементы игры, шутки, некоторые решения просто красивы.
При желании вы можете ознакомиться с правильными ответами в заключительном разделе. Не забудьте использовать четыре составляющие основной стратегии. Со временем у вас выработается собственный стиль, который будет помогать вам при решении различных задач.
Сортировка задачи
УПРАЖНЕНИЕ.
Если три дня назад был день, предшествующий понедельнику, то какой день будет послезавтра?
Первый шаг в решении задачи - выяснить, в чем же, собственно, она состоит. Если вы сформулируете, что вы на самом деле ищете, то у вас сразу же появится и конечная цель, и некая исходная точка. Итак, попробуем определить, какой день будет послезавтра. Перед понедельником было воскресенье. Если три дня назад было воскресенье, то сегодня - среда.
Если сегодня - среда, значит, послезавтра будет пятница.
Иногда задача становится совершенно тривиальной, если правильно рассортировать информацию. В следующих загадках начните с определения цели, а затем сформулируйте загадку таким образом, чтобы к ней легче было подступиться.
- В зоопарке имеются тридцать голов и сто ног. Сколько зверей и сколько птиц живут в зоопарке?
- Три миссионера и три каннибала должны пересечь реку в лодке, в которой могут поместиться только двое. Миссионеры должны соблюдать осторожность, чтобы каннибалы не получили на каком-то берегу численное преимущество. Как переплыть реку?
- Криптарифм - это задача, в которой требуется расшифровать какие-то арифметические действия. В большинстве криптарифмов каждая цифра зашифрована своей буквой. Два замечательных криптарифма, изображенные ниже, вносят приятное разнообразие в установившиеся каноны, но легко решаются с помощью логических рассуждений и допускают лишь один-единственный ответ.
, , E, E, O, , , , , , , P, P, P
, , , O, O, , , , , , , , P, P
, E, O, E, O, , , , , , P, P, P, P
, E, O, O, , , , , , P, P, P, P,
O, O, O, O, O, , , , , P, P, P, P, P
В обеих задачах умножаются какие-то два числа. В левой задаче каждая буква Е означает четную цифру, буква О - нечетную. Разумеется, из того, что все четные цифры обозначены одной и той же буквой Е, еще не следует, что все четные цифры одинаковы. Одна буква Е может означать цифру 2, другая - 4 и так далее. Нуль считается четной цифрой. Требуется расшифровать весь пример.
В правой задаче каждая буква Р означает какое-нибудь простое однозначное число (2, 3, 5 или 7). - Трое приятелей кидают монету, причем проигравший платит выигравшим столько, сколько они уже выиграли. После трех партий каждый проиграл по разу и каждый имеет по тридцать шесть долларов. С каких сумм они начали?
- Миранда обыграла Розмари в теннис со счетом 6:3. В пяти играх победу одерживает та из девушек, которая не подает. Чьей была первая подача?
- Из ведра, содержащего 5 литров воды, отливают 1 литр, а затем в ведро вливают 1 литр сока. Перемешав все это, из ведра отливают 1 литр смеси, затем в ведро опять вливают 1 литр сока. Опять перемешивают, отливают 1 литр смеси и вливают 1 литр сока. Сколько в ведре после этого останется воды?
Иллюстрации Хороший способ решать задачи - рисовать к ним иллюстрации. Рисунок - даже простая схема или диаграмма - позволяет наглядно представить задачу, а значит, расширяет ваши возможности поработать над решением. Опытный логик, без сомнения, понимает важность графического комментария к задаче.
С помощью карандаша и листа бумаги можно записать всю информацию, какой вы только располагаете по данной проблеме, и представить эту информацию в удобной для вас форме. Вот пример:
- Однажды утром, как раз в тот момент, когда взошло солнце, один буддийский монах начал восхождение на высокую гору. Узкая тропа шириной не более одного-двух футов вилась серпантином по склону горы к сверкающему храму на ее вершине.
Монах шел по дорожке то быстрее, то медленнее; он часто останавливался, чтобы отдохнуть и поесть сушеных фруктов, которые взял с собой. К храму он подошел незадолго до захода солнца. После нескольких дней поста и размышлений монах пустился в обратный путь по той же тропе.
Он вышел на рассвете и опять спускался с неравномерной скоростью, неоднократно отдыхая по дороге. Средняя скорость спуска, конечно, превышала среднюю скорость подъема.
Докажите, что на тропе есть такая точка, которую монах во время спуска и во время подъема проходил в одно и то же время суток.
Решить эту задачу очень просто, если нарисовать схему.
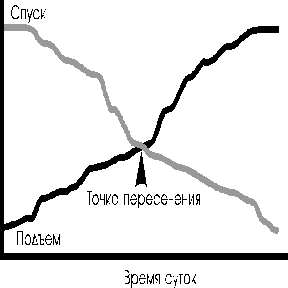
Путь монаха можно представить в виде графика в координатах время-высота. Когда вы наложите друг на друга обе траектории пути, вы увидите, что искомая точка действительно существует, причем только одна.
- Поиск шаблонов
- Задачи - это полоса препятствий
- Порочный круг
- Смотрите на вещи вверх тормашками.
- Зацепки
