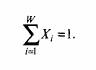На практике число ценных бумаг в портфеле всегда конечно, и поэтому распределение инвестиций по различным ценным бумагам может лишь
уменьшить риск, но не исключить его полностью.
Итак, при определении риска конкретного портфеля ценных бумаг
необходимо учитывать корреляцию курсов акций. В качестве показателя
корреляции Г. Марковитц использует ковариацию С, между изменениями
курсов отдельных ценных бумаг.
Таким образом, дисперсия всего портфеля рассчитывается по следующей
формуле:
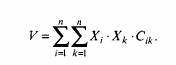
По определению, при i = к С., равно дисперсии акции. Это означает,
что дисперсия, а значит, и риск данного портфеля зависят от риска
данной акции, ковариации между отдельными акциями (систематического
риска рынка) и долей Z. отдельных ценных бумаг в портфеле в
целом.
Рассматривая теоретически предельный случай, при котором в портфель
можно включать бесконечное количество ценных бумаг, дисперсия
асимптоматически будет приближаться к среднему значению ковариации С.
Графически это можно представить в виде рис. 2
Г. Марковитц разработал очень важное для современной теории портфеля
ценных бумаг положение, которое гласит: совокупный риск портфеля
можно разложить на две составные части. С одной стороны, это
так называемый систематический риск, который нельзя исключить и
которому подвержены все ценные бумаги практически в равной степени.
С другой — специфический риск для каждой конкретной ценной бумаги,
который можно избежать при помощи управления портфелем ценных
бумаг. При этом сумма вложенных средств по всем объектам должна
быть равна общему объему инвестиционных вложений (например,
часть средств на банковском счете вводится в модель как инвестиция с
нулевым риском), т.е. сумма относительных долей X. в общем объеме
должна равняться единице: