Таким образом, риск выражается отклонением (причем более низких!) значений доходов от наиболее вероятного значения. Мерой рассеивания является среднеквадратичное отклонение а,, и чем больше это значение, тем больше риск:
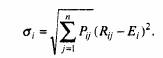
в модели Марковитца для измерения риска вместо среднеквадратичного
отклонения используется дисперсия D,, равная квадрату а так
как этот показатель имеет преимущества по технике расчетов:
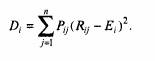
Инвестора, желающего оптимально вложить капитал, интересует не
столько сравнение отдельных видов ценных бумаг между собой, сколько
сравнение всевозможных портфелей, так как это позволяет использовать
эффект рассеивания риска, т.е. определяется ожидаемое значение
дохода и дисперсия портфеля. Ожидаемое значение дохода Е портфеля
ценных бумаг определяется как сумма наиболее вероятных доходов Е-
различных ценных бумаг п. При этом доходы взвешиваются с относительными
долями Xj (i = ... «), соответствующими вложениям капитала
в каждую облигацию или акцию:
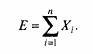
Для дисперсии эта сумма применима с определенными ограничениями,
так как изменение курса акций на рынке происходит не изолированно
друг от друга, а охватывает весь рынок в целом. Поэтому дисперсия
зависит не только от степени рассеяния отдельных ценных бумаг, а также
от того, как все они в совокупности одновременно понижаются или
повышаются по курсу, т.е. от корреляции между изменениями курсов
отдельных ценных бумаг. При сильной корреляции между отдельными
курсами (если все акции одновременно повышаются или понижаются)
риск за счет вкладов в различные ценные бумаги нельзя ни уменьшить,
ни увеличить. Если же курсы акций абсолютно не коррелируют между
собой, но в предельном случае (портфель содержит бесконечное число
акций) риск можно было бы исключить полностью, так как колебания
курсов в среднем были бы равны нулю.
