Недостатков можно избежать, используя континуальную версию критерия VaR. Интересы инвестора при этом описываются неубывающей функцией критических доходов Bcr(e), eÎ[0,1]. Эта функция может принимать и отрицательные значения. Более того, она может быть неограниченной в обоих концах отрезка [0,1]. Требуется построить стратегию инвестора, в соответствии с которой его доход B от инвестиции в размере A окажется не ниже Bcr(e) с вероятностью не меньше 1 – e для каждого eÎ[0,1], т.е.
, 
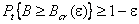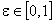. (1)Если такая задача может быть решена полностью, то остающаяся после ее решения сумма направляется на максимизацию среднего дохода, т.е. инвестируется в инструмент D(Emax) с возможным использованием короткой позиции по инструменту D(Emin).
Каждому уровню вероятности eÎ[0,1] соответствует критическое множество X(e) вероятностной меры инвестора e и его рыночная вероятность g(e). X(e) – неубывающее по параметру e семейство множеств, g(e) – непрерывная и неубывающая функция e, g(e) > e для всех eÎ(0,1), g(0) = 0, g(1) = 1. Решение задачи дается следующей процедурой.
Рассматривается непрерывный процесс инвестирования суммы A по мере возрастания параметра e от 0 до 1. Через A(e) обозначим инвестиционную сумму, необходимую для реализации (6) до произвольной фиксированной точки e включительно (т.е. обеспечения доходов Bcr(e') на множествах
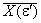соответственно для всех 
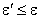). Тогда справедлива формула (имеющая смысл при Bcr(0) > –¥)
.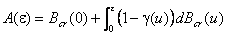