Задача безусловной максимизации среднего дохода инвестора состоит в том, чтобы для заданной инвестиционной суммы A подобрать в качестве объекта инвестирования некоторый инструмент G с платежной функцией g(x), удовлетворяющий равенству G = A и доставляющий максимум MtB.
Разумеется, такая задача представляет интерес лишь для нейтрального к риску инвестора. Если рассматривать случай, когда инвестор использует лишь инструменты, которые не могут приносить ему отрицательные доходы, т.е. используются лишь инструменты с неотрицательными платежными функциями, то оказывается, что решение задачи доставляют инструменты из класса D(E). При этом условие неотрицательности доходов инвестора означает, что по этим инструментам он фактически может использовать лишь длинные позиции. Для таких инструментов имеет место
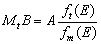 .
.Для обоснования этого вводятся функции правдоподобия
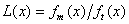 ,
,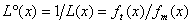 ,
,составляющие основу применяемого в статистике критерия Неймана-Пирсона (см., например, [4]).
Процедура Неймана-Пирсона позволяет утверждать, что средний доход инвестора принимает наибольшее значение при страйке Emax, доставляющем наибольшее значение функции правдоподобия L°. Любая другая платежная функция приносит меньший средний доход.
Задача безусловной максимизации среднего дохода не учитывает рисковых предпочтений инвестора. К тому же, очевидно, что предоставляемое инструментом D(Emax) решение не удовлетворительно: доход инвестора равен нулю с вероятностью 1 и бесконечности – с вероятностью нуль, т.е. случайный доход вырожден. Если же говорить о практической реализации этого решения, то речь идет о том, что максимизация среднего дохода инвестора достигается за счет получения весьма больших случайных доходов с незначительной вероятностью и нулевых доходов со значительной вероятностью.
Использование коротких позиций по инструменту D(Emin), где Emin обозначает страйк, доставляющий L° минимум (или же L – максимум), позволяет сколь угодно повысить доходность инвестиции.
мЮВЮКН

