Далее мы будем считать, что введенные в предыдущем разделе вероятностные характеристики будущей цены базового актива нам неизвестны. Если оставаться в условиях нейтрального к риску рынка, то по формуле (1) можно было бы восстанавливать плотность вероятности f(x) (с одновременным определением и параметра r). Но теперь мы желаем отказаться от предположения нейтральности к риску рынка. Тем самым мы признаем, что формулы предыдущего раздела не выполняются (во всяком случае, они не дают точного значения стоимости опционов) и восстановить по ним точно f(x) невозможно.
Поэтому далее для решения проблем инвестора мы оставляем в стороне вопросы ценообразования опционов. Оказывается, что для целей нахождения оптимального портфеля инвестора нет необходимости знать работу механизма ценообразования. Достаточно просто знать сами цены опционов. Однако подчеркнем еще раз, что для решения задачи в ее теоретической полноте потребуется предположение о наличии на рынке опционов со страйками из множества всех вещественных чисел (эти страйки будут многомерными в случае многопериодных опционов).
Итак, сложившиеся на начало периода цены опционов будем воспринимать как данность. Конечно, они должны удовлетворять определенным свойствам, вытекающим из общего финансового принципа недопустимости арбитража.
Из формулы (1) следует, что
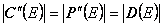 .
.Хотя инструменты C"(E) и P"(E) получены различными способами, естественно считать, что их стоимости совпадают, так как в противном случае был бы возможен арбитраж. Итак, имеем
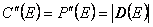 .
.Поскольку инструменту D(E) отвечает неотрицательная платежная функция, то его стоимость не может быть отрицательной, т.е.
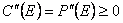 .
.Следовательно, цены колла и пута как функции страйка – выпуклы.
