Отметим, что наведенные совместные плотности вероятности, соответствующие различным временным горизонтам, должны быть согласованы между собой. Именно из условия невозможности арбитража вытекает, что должно быть выполнено рекуррентное по k < n соотношение
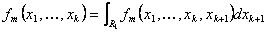 . (3)
. (3)Действительно, как следует из соотношения (16), обе наведенные плотности, входящие в эту формулу, означают стоимость инструмента D(E1, E2,…, Ek), помноженную на
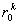 , и инструмента D(E1, E2,…, Ek+1), помноженную на
, и инструмента D(E1, E2,…, Ek+1), помноженную на 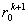 , соответственно. Интегрирование второй стоимости по всем Ek+1 дает стоимость первого инструмента, но с отсрочкой платежа по нему на один период. Условие недопущения арбитража требует, чтобы эти стоимости различались множителем
, соответственно. Интегрирование второй стоимости по всем Ek+1 дает стоимость первого инструмента, но с отсрочкой платежа по нему на один период. Условие недопущения арбитража требует, чтобы эти стоимости различались множителем 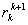 , который в соответствии с (17) равен
, который в соответствии с (17) равен 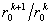 . Последнее обстоятельство и подтверждает справедливость предположения (18).
. Последнее обстоятельство и подтверждает справедливость предположения (18).Соотношение (18) означает, что система наведенных совместных плотностей вероятности обладает свойством согласованности, присущим системам обычных совместных плотностей. Кроме того, оно же говорит о том, что в n-периодных зависящих от пути опционах содержится почти вся информация относительно распределения вероятностей для последовательности цен базового актива длины n, за исключением лишь информации о последовательности безрисковых относительных доходов за отдельные периоды всего интервала инвестирования. Кстати, очевидно также, что для полноты рынка вовсе не нужно требовать наличия на рынке зависящих от пути опционов сроков действия меньше n – достаточно обычных k-периодных опционов для всех k<n, поскольку из них также можно получить все ставки – как спотовые, так и форвардные. Более того, эти опционы (если рассуждать чисто теоретически) нужны лишь как источник информации о процентных ставках по периодам.
