Если предполагать рынок нейтральным к риску, то аналогично однопериодному случаю можно предложить формулу ценообразования A-опционов. Так, для варианта A-опциона с вектором a°, все компоненты которого равны +1, естественно положить
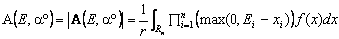 , (1)
, (1)Г
де r – относительный доход от инвестиции за весь горизонт инвестирования.
Дифференцируя по всем переменным xi однократно и двукратно, получим стоимости "первой производной" и "второй производной" этого A-опциона соответственно (еще раз подчеркнем, что фактически речь идет о смешанных производных n-го и 2n-го порядков соответственно):
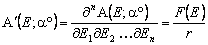
и
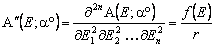 .
.Из равенства (13) нетрудно получить соотношение, обобщающее формулу (2) из [1], задающую стоимость опциона пут через функцию распределения цены актива. Если обозначить через Rn(E) квадрант {x xi £ Ei, i Î T} n-мерного евклидова пространства Rn, то равенство (13) можно записать в виде
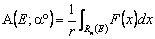 .
.