Остается вспомнить, что в силу обоснованно предполагаемой согласованности цен A-опционов (в случае, если области существования котировок разных A-опционов перекрываются) и функция fm(x), и параметр
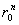не зависят от a. И, наконец, очевидное равенство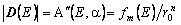
в сочетании с формулой (12) дает соотношение
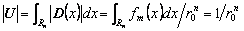,означающее, что нормировочный коэффициент
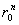равен безрисковому относительному доходу за весь n-периодный горизонт инвестирования.Далее, зависящие от пути опционы со сроками действия меньше n, которые также могут присутствовать на рынке (и такую возможность мы будем предполагать), определяют свои наведенную рынком совместную плотность вероятности fm(x), x = (x1, x2,…, xk), k<n, и наведенный рынком безрисковый относительный доход
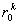за первые k периодов. При этом важно, что наведенные безрисковые относительные доходы для горизонтов различной длительности определяются лишь из опционов соответствующей фактической длительности, при этом формально никакого согласования между ними не требуется. Иными словами, в ценах k–периодных опционов на момент времени t = 0 содержится информация лишь об относительном доходе 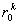, но они ничего не говорят о распределении наращивания этого дохода по периодам. Поэтому для полноты n-периодного рынка следовало бы потребовать, чтобы на нем котировались A-опционы всех сроков действия k £ n.По совокупности наведенных рыночных спотовых безрисковых относительных доходов
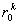, k = 1, 2,…, n, могут быть определены и форвардные безрисковые относительные доходы для любого форвардного срока. Так, наведенный форвардный относительный доход 
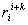за интервал длительности k периодов через i периодов от начального момента времени t = 0 (т.е. отсчитывая интервал от момента t = i) составит
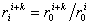. (2)
