Как мы уже отмечали, "вторые производные" всех A-опционов имеют одну и ту же платежную функцию (11) (независимо от a). И потому их стоимости на нашем рынке должны совпадать между собой и удовлетворять равенству
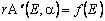 .
.Это соотношение следует также из формулы (15) – смешанные производные по всем страйкам от всех слагаемых в правой части равенства, кроме первого, равны нулю!
Можно получить и аналог теоремы паритета опционов. В данном случае она менее наглядна и едва ли имеет практическое значение. Тем не менее аналог этой теоремы имеет теоретическое значение и, безусловно, является обобщением. Именно имеет место равенство
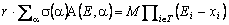 .
.Для доказательства заметим, что
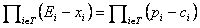 ,
,где pi = max(0, Ei–xi), ci = max(0, xi–Ei). При перемножении n сомножителей в правой части равенства получаем 2n слагаемых, каждое из которых соответствует платежной функции некоторого A-опциона, а знак определяется четностью или нечетностью вхождений в слагаемое сомножителей типа ci, а именно значением s(a). Беря математическое ожидание от произведения, получаем теорему паритета.
