Аналогично для получения "вторых производных" следует брать смешанные производные по всем страйкам, но уже по каждому – вторую. Нетрудно видеть, что платежные функции "вторых производных" всех типов A-опционов с одинаковым векторным страйком E совпадают между собой и являются n-мерными дельта-функциями относительно E, т.е. для любого вектора a инструмент "дельта-функция" определяется равенством
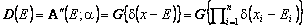 . (3)
. (3)Отметим, что именно совпадение "вторых производных" всех типов A-опционов между собой делает необязательным их одновременное присутствие на теоретическом рынке для любого E.
С помощью "дельта-функции" D(E1, E2,…, En) формальное представление инструмента G{g(x)} с произвольной платежной функцией n переменных g(x) = g(x1, x2,…, xn) можно задать в виде
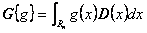 . (4)
. (4)Очевидно, что обычный n-периодный опцион может быть рассмотрен как частный случай зависящего от пути n-периодного опциона и потому получен из A-опционов (например, использованием формулы (12)). Менее очевидна связь опционов с разными сроками действия. Имеет смысл сопоставить зависящие от пути n-периодные опционы с зависящими от пути k-периодными опционами, k < n, и, в частности, с обычными k-периодными опционами, для которых платежная функция определяется лишь ценой актива в момент времени t = k.
Отметим следующее. Для репликации k-периодных опционов с помощью n-периодных зависящих от пути опционов можно, исходя из платежных функций n-периодных зависящих от пути опционов, построить функции n переменных, фактически зависящие лишь от первых k переменных. Это всегда можно сделать, используя введенные "производные" от базисных n-периодных A-опционов. Поэтому может показаться, что эти функции могут служить платежными функциями k-периодных опционов и что, следовательно, задача реализации k-периодных опционов из n-периодных опционов, в принципе, разрешима.
Однако это не совсем так. Различие, и неустранимое, все же остается. Оно состоит в сроках расчета по опционам. По k-периодным опционам расчет производится в момент k, а по n-периодным – в момент n. Можно сказать, что зависящий от пути n-периодный опцион с платежной функцией, определяемой ценами актива в моменты времени t £ k, идентичен некоторому зависящему от пути (или обычному) опциону с k-периодным сроком действия, но с задержкой расчетов до окончания процесса инвестирования (t = n), и потому требует учета накопленных процентов.
Тем не менее, когда на рынке присутствуют зависящие от пути (или обычные) опционы с разными сроками действия, их стоимости должны быть некоторым образом согласованы – иначе возможен временной арбитраж! Далее эта согласованность будет уточнена.
