После интегрирования по частям получаем соотношение общего вида, не требующее конечности Bcr(0),
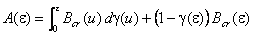.При
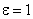эти формулы приобретают вид
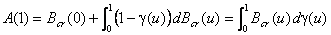,причем средняя часть этого двойного равенства снова имеет смысл лишь при Bcr(0) > –¥. Процесс достигает точки e, если A(e) £ A.
Если это неравенство нарушается в некоторой точке отрезка [0,1], процесс прекращается. Если же процесс не обрывается вплоть до точки
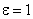, т.е. оказывается, что
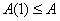, (2)то это значит, что ограничения (6) выполняются для всех eÎ[0,1], и тогда сумма A – A(1) направляется на максимизацию среднего дохода, т.е. вкладывается в инструмент D(Emax).
Случайный доход инвестора B может быть представлен как сумма двух случайных величин
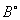и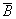 
, первая из которых фактически является вырожденной случайной величиной, принимающей бесконечно большое значение с бесконечно малой вероятностью и равной нулю с вероятностью 1, а вторая – случайная величина, отвечающая исключительно за выполнение ограничений метода VaR. При этом из неравенства (6) следует, что функция распределения случайной величины 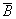задается равенством
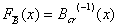,правую часть которого образует обратная к Bcr(e) функция.
