Ранжирование элементов, анализируемых с использованием матрицы парных сравнений [E], осуществляется на основании главных собственных векторов, получаемых в результате обработки матриц.
Вычисление главного собственного вектора W положительной квадратной матрицы [E] проводится на основании равенства
EW=λmaxW, (2.1)
где λmax — максимальное собственное значение матрицы [Е].
Для положительной квадратной матрицы [Е] правый собственный вектор W, соответствующий максимальному собственному значению λmax, с точностью до постоянного сомножителя С можно вычислить по формуле
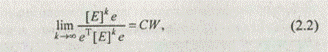
где е={1,1,1, ....l}Т – единичный вектор;
k = 1, 2, 3, ... — показатель степени;
С— константа;
Т — знак транспонирования.
Вычисления собственного вектора W по выражению (2.2) производятся до достижения заданной точности:
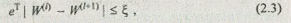
где l — номер итерации, такой, что l = 1 соответствует k = 1; l = 2, k = 2;
l = 3, k = 4 и т. д.;
ξ — допустимая погрешность.
С достаточной для практики точностью можно принять x = 0,01 независимо от порядка матрицы.
Максимальное собственное значение вычисляется по формуле:
λmax=eT[E]W
