Все три уравнения эквивалентны. Решение можно получить методом итераций.
Зная для нашего геометрического оптимального портфеля GHPR= 1,01542 и соответствующее AHPR= 1,031 и решая любое уравнение с (7.10а) по (7. 10г), мы находим, что N = 83,49894. Таким образом, после того, как пройдет 83,49894 сделки, геометрическое TWR догонит арифметическое. Полученный результат справедлив для тех TWR, которые соответствуют координате дисперсии геометрического оптимального портфеля.Так же, как и AHPR, GHPR имеет свою линию CML. Рисунок 7-5 показывает как AHPR, так и GHPR с линиями CML, рассчитанными на основе безрисковой ставки.
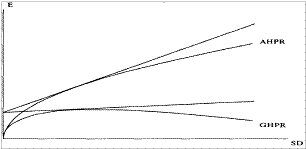
Рисунок 7-5 AHPR, GHPR и их линии CML
Зная CML для AHPR, можно рассчитать CML для GHPR следующим образом:
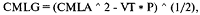
CMLG = координата Е (по вертикали) линии CML для GHPR при данной координате V, соответствующей Р;
CMLA= координата Е (по вертикали) линии CML для AHPR при данной координате V, соответствующей Р;
Р = процент в касательном портфеле, рассчитанный из (7.02);
VT = координата дисперсии касательного портфеля.
Следует иметь в виду, что для данной безрисковой ставки касательный портфель и геометрический оптимальный портфель в общем случае не одинаковы. Портфели будут идентичными при выполнении следующего равенства:
(7.12) RFR=GHPROPT-1,
где RFR = безрисковая ставка;
GHPROPT = среднее геометрическое HPR геометрического оптимального портфеля, т.е. координата Е портфеля на эффективной границе.
Только когда разность GHPR геометрического оптимального портфеля и единицы равна безрисковой ставке, геометрический оптимальный портфель и касательный портфель будут одинаковыми. Если RFR > GHPROPT - 1, тогда геометрический оптимальный портфель будет слева (т.е. иметь меньшую дисперсию, чем касательный портфель). Если RFR < GHPROPT - 1, тогда касательный портфель будет слева (т.е. иметь меньшую дисперсию, чем геометрический оптимальный портфель). Во всех случаях касательный портфель, конечно же, никогда не будет иметь более высокое GHPR, чем геометрический оптимальный портфель.
Отметьте также, что точки касания CML к GHPR и CML к AHPR имеют одну координату SD. Мы можем использовать уравнение (7.01а) для поиска касательного портфеля GHPR, заменив в (7.01а) AHPR на GHPR. В результате получится следующее уравнение:
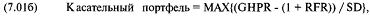
где МАХ{}= максимальное значение;
GHPR = геометрическое среднее HPR, т.е. координата Е данного портфеля на эффективной границе;
SD = стандартное отклонение HPR, т.е. координата SD данного портфеля на эффективной границе;
RFR = безрисковая ставка.
мЮВЮКН

