Что касается вида j(SТ), то удобно искать эту функцию в виде плотности гауссовского распределения с нечеткими параметрами среднего и среднеквадратического отклонения, как это обосновывается. Тогда (5.24) имеет вид усеченной слева плотности нормального распределения с нечеткими параметрами, с дельта-функцией на левом конце распределения, бимодальной формы (рис. 3.5).
Введем бимодальную функцию самого общего вида, которую далее будем называть функцией вида H(v0 , v1) .
Для нее значение v0 , определяемое (3.26) – это абсцисса левого максимума плотности дельта-функции;
v1 – абсцисса правого максимума плотности распределения, определяемая по формуле
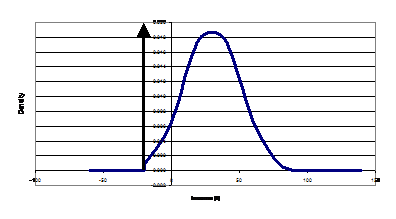
Рис. 3.5. Плотность распределения доходности сборки
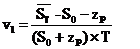
где