Коэффициент пропорциональности в (3.20) есть не что иное, как хорошо известный в портфельном менеджменте показатель Шарпа – отношение доходности индекса (за вычетом безрисковой составляющей доходности) к волатильности индекса. Только в нашем случае он имеет нечеткий вид, сводимый к треугольному по правилу:
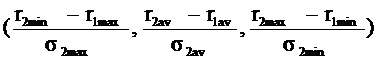
В таблицу 3.5 сведены границы для модельного класса облигаций в структуре модельного портфеля для различных уровней риска.
Таблица 3.5. Оптимальная доля облигаций в портфеле
|
Риск портфеля, % год |
1 |
5 |
10 |
15 |
20 |
25 |
30 |
|
|
Доля облигаций в портфеле |
max |
0.967 |
0.833 |
0.667 |
0.500 |
0.333 |
0.167 |
0.000 |
|
av |
0.960 |
0.800 |
0.600 |
0.400 |
0.200 |
0.000 |
0 |
|
|
min |
0.950 |
0.750 |
0.500 |
0.250 |
0.000 |
0 |
0 |
|
|
Разброс |
0.067 |
0.083 |
0.167 |
0.250 |
0.333 |
0.167 |
0 |
|
По краям полосы разброс портфельных границ ниже, чем в середине. Это объясняется тем, что на краях полосы эффективной границы портфель обладает вполне определенным стилем: большей доходности отвечает модельный класс акций, а меньшему риску – модельный класс облигаций.
