Таким образом, портфель описан системой статистически связанных случайных величин с нормальными законами распределения. Тогда, согласно теории случайных величин, ожидаемая доходность портфеля r находится по формуле
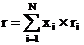
а стандартное отклонение портфеля s -
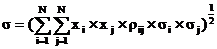
Задача управления таким портфелем имеет следующее описание: определить вектор {xi}, максимизирующий целевую функцию r вида (3.12) при заданном ограничении на уровень риска s, оцениваемый (3.13):
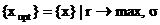
где sM – риск бумаги с максимальной среднеожидаемой доходностью.
Запись (3.14) есть не что иное, как классическая задача квадратичной оптимизации, которая может решаться любыми известными вычислительными методами.
Замечание.
В подходе Марковица к портфельному выбору под риском понимается не риск неэффективности инвестиций, а степень колеблемости ожидаемого дохода по портфелю, причем как в меньшую, так и в большую сторону. Можно без труда перейти от задачи вида (3.14) к задаче, где в качестве ограничения вместо фиксированного стандартного отклонения выступает вероятность того, что портфельная доходность окажется ниже заранее обусловленного уровня.
