В полном соответствии, определим лингвистическую переменную «Оценка бумаги» с терм-множеством значений «Очень низкая (О), Низкая (Н), Средняя (Ср), Высокая (В), Очень высокая (ОВ)». Чтобы конструктивно описать введенную лингвистическую переменную «Оценка бумаги», определим носитель ее терм-множества – действительную переменную A_N на интервале от нуля до единицы. Тогда функции принадлежности соответствующих нечетких подмножеств могут быть заданы таблично (таблица П3.6);
Определим лингвистическую переменную «Торговая рекомендация для бумаги» с терм-множеством значений «Strong Buy (SB – Определенно Покупать), Moderate Buy (MB – Покупать под вопросом), Hold (H – Держать), Moderate Sell (MS – Продавать под вопросом), Strong Sell (SS – Определенно продавать)».
Установим взаимно однозначное соответствие введенных нами лингвистических переменных на уровне подмножеств: ОН – SS, Н – MS, Ср – H, В – MB, ОВ – SB. Так мы связали качество ценной бумаги с ее инвестиционной привлекательностью. Тогда переменная A_N является носителем и для терм-множества лингвистической переменной «Торговая рекомендация», с теми же функциями принадлежности носителя подмножествам значений.
Оценим веса отдельных факторов для комплесксной оценки бумаги, в соответствии с тем, как это записано в (2.10). Согласно правилу точечных оценок Фишберна, критерию максимума неопределенности в части наличной информационной ситуации (по аналогии с тем, как это оценивается в [95, 98]) можно сопоставить следующую систему весов:
p1 = 0.3, p2 = p3 = 0.15, p4 = p5 = p6 = p7 = p8 = 0.08, 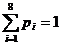
Если в качестве носителя лингвистической переменной «Уровень показателя Х» выбрать единичный интервал, то трапециевидные функции правдоподобия будут иметь вид рис. П3.9;
Тогда, по аналогии с тем, как это сделано в [53, 64], получем комплексный показатель A_N для каждой бумаги методом двойной свертки:
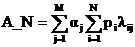
где i – индекс отдельного показателя для их общего числа N=8,
j – индекс уровня показателя для общего числа уровней M=3,
lij – ранг i-го показателя по своему j-ому уровню, определяемый таблицами П3.3 – П3.5,
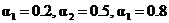
абсциссы максимумов функций принадлежности терм-множества лингвистической переменной «Уровень фактора» (см. рис. П3.9).
