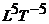Квантовое описание требуется тогда, когда изменение энергии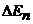 
, оказывается соизмеримым с самой энергией 
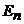
. Если же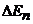 
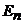
исчезает и имеется классический случай с интегрируемым законом сохранения (1).
Дальнейшее развитие квантовой теории привело к квантовой механике Шредингера, в которой, стационарное состояние, т.е. состояние, имеющее определенную энергию, описывается волновой функцией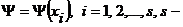 
=
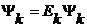
- эрмитов оператор Гамильтона, причем 
, где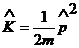 
- эрмитов оператор импульса,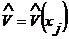 
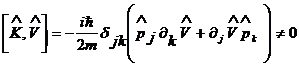, то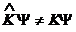 
, т.е. кинетическая и потенциальная энергия не будут иметь определенных значений. Тогда вместо интегрируемого закона сохранения энергии (1) имеется неинтегрируемый закон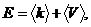 
- среднее значение 
. При этом можно говорить, только о вероятностях того, что, если система находится в стационарном состоянии с энергией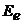 
, а потенциальная 
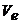
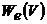
и 
и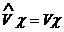 
и операторов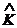 
разложить их по 
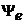
. Тогда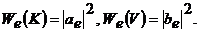 
таблицы ди Бартини-Кузнецова. Действительно, т.к .
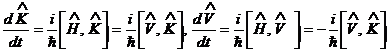
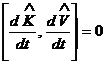
а значит изменения кинетической и потенциальной энергий можно определить одновременно, в то время как сами кинетическую и потенциальную энергию определить нельзя. Но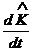 
– инварианты из клетки
