Приобретая опцион put, инвестор рассчитывает получить премию как разницу между ценой исполнения опциона xp и финальной ценой подлежащего актива ST. Если эта разница перекрывает цену приобретения опциона zp, то владелец опциона получает прибыль. В противном случае имеют место убытки.
Надо сказать, что приобретение опциона put без покрытия подлежащим активом не является традиционной стратегий. Классический инвестор все же психологически ориентируется на курсовой рост приобретаемых активов. С этой точки зрения стратегия классического инвестора – это стратегия «быка». А покупка put опциона без покрытия – эта «медвежья» игра.
Обычная логика использования опциона put – это логика отсечения убытков с фиксацией нижнего предела доходности, который не зависит от того, насколько глубоко провалился по цене подлежащий актив. Но для нас не имеет значения, какой стратегии придерживается инвестор. Мы понимаем, что опцион put является потенциальным средством извлечения доходов, и нам эту доходность хотелось бы вероятностно описать.
Проведем рассуждения по аналогии с предыдущим разделом работы. Случайная величина дохода по опциону связана со случайной величиной финальной цены подлежащего актива соотношением [7.2]
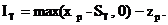
А текущая доходность по опциону put определяется формулой
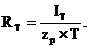
Используем все соображения о получении плотностей распределения, выработанные в предыдущем разделе работы. В нашем случае, исходя из (22)

|dST/dIT| = 1, IT > -zp. (7.25)
