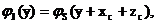Определим плотность jI(y) распределения дохода IT по опциону как функции случайной величины ST. Воспользуемся известной формулой. Если исходная случайная величина X имеет плотность распределения jX(x), а случайная величина Y связана с X функционально как Y=Y(X), и при этом существует обратная функция X=X(Y), тогда плотность распределения случайной величины Y имеет вид [7.6]
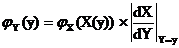
В нашем случае, исходя из (7.5),
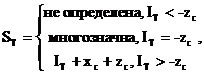
dST/dIT = 1, IT > -zc. (7.9)
Мы видим, что в точке IT = -zc плотность jI(y) приобретает вид дельта-функции. Необходимо определить множитель при дельта-функции. Это можно сделать косвенным образом. На участке, где функция ST(IT) дифференцируема, в силу (7.7)-( 7.9) выполняется