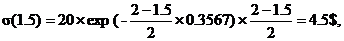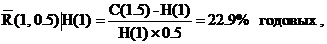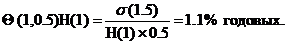Облигация номиналом N = 1000$ выпускается в обращение в момент времени TI = 0 (далее все измерения времени идут в годах) сроком на 2 года c дисконтом 30%, то есть по эмиссионной цене N0 = 700$. Инвестор намеревается приобрести бумагу в момент времени t =1. В этот момент текущая цена бумаги на рынке составляет H(1) = 820$. Для проведения статистического анализа доступна история сделок с бумагой за истекший год ее обращения. Требуется идентифицировать доходность облигации R(t=1, T) на протяжении оставшегося года владения ( T Î [0, 1] ) как случайный процесс и определить параметры этого процесса.
Решение
Согласно (6.6), (6.7), внутренняя норма доходности нашей облигации составляет
r = ln(1000/700) = 35.67% годовых, (6.15)
а справедливая цена
С(t) = 1000*exp(-(2-t)*0.3567/2), t Î [0, 2]. (6.16)
Далее следует этап анализа истории цены за истекший год. СКО шума цены, согласно (6.9), имеет вид
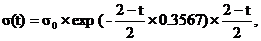
где s0 определяется на основе анализа истории скорректированного шума цены вида (6.11).
Теперь бумага полностью идентифицирована. Случайный процесс ее доходности имеет параметры, которые определяются по формулам (6.13), (6.14).
В частности, на момент погашения бумаги Т = 1,
C(2) = 1000$, s(1+1) = 0, e(1+1) = 0, и
R(1,1) = (1000-820)/(820*1) = 21.95% годовых – неслучайная величина.
Оценим процесс количественно через Т = 0.5 лет владения бумагой, задавшись параметром СКО шума s0 = 20$. Тогда
C(1.5) = 1000*exp(-(2-1.5)*0.3567/2) = 914.7$, (6.18)