В начале года инвестор приобретает за zc = 10 ед. цены опцион call на подлежащий актив со стартовой ценой S0 = 100 ед. Цена исполнения опциона xc = 100 ед., опцион американский, срочностью 1 год. Поскольку цена исполнения совпадает со стартовой ценой, то покупаемый опцион является опционом в деньгах. Инвестор ориентируется на следующие параметры доходности и риска подлежащего актива: текущая доходность r = 30% годовых, СКО случайной величины текущей доходности sr = 20% годовых. В пересчете на финальную цену ST это означает, что через время Т = 0.5 лет подлежащий актив будет иметь нормальное распределение ST с параметрами sT = 115 ед. и sS = 10 ед. Требуется определить доходность и риск опциона в момент времени Т = 0.5 года.
Решение
Все полученные соотношения реализованы в компьютерной программе.
Расчет по формулам (7.16) - (7.18) дает QT = 0.335, 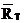
Одновременно отметим: поскольку вероятность того, что опцион не в деньгах, мала (0.066), то полученные значения моментов близки к своим асимптотическим приближениям (7.21) 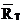
Результаты наглядно показывают то, что опцион – это одновременно высокорисковый и высокодоходный инструмент. Высокая доходность достигается за счет левериджа: не вкладывая деньги в подлежащий актив, инвестор тем не менее получит по нему возможный доход и не будет участвовать в убытках. Другое дело, что обычно инвестор балансирует на грани прибылей и убытков, ибо все ищут выигрыша, и никто не станет работать себе в убыток. Поэтому для call-опционов в деньгах разница между среднеожидаемой ценой подлежащего актива и ценой приобретения опциона обычно колеблется вокруг цены исполнения. Это означает, что вложения в непокрытые опционы с точки зрения риска сопоставимы с игрой в орлянку. Для put опциона в деньгах сопоставимыми являются цена исполнения, с одной стороны, и сумма цены опциона и ожидаемой цены подлежащего актива – с другой стороны.
