Обозначим плотность этого распределения
j(r,m,s),
где r – расчетное значение доходности.
Однако, если пронаблюдать фактическое ценовое поведение акций и паев взаимных фондов, то мы увидим, что доходность этих активов не колеблется вокруг постоянной случайной величины, но образует динамический тренд. Поэтому винеровская модель в чистом виде применяется крайне редко и на временных интервалах малой длительности.
Применим соображения, которые мы выдвинули в главе 2 книги, для приведения винеровской модели к нечетко-множественному виду.
Пусть у нас есть квазистатистика доходностей (r1, …rN) мощности N и соответствующая ей гистограмма (n1,...,nM) мощности M. Для этой квазистатистики мы подбираем двупараметрическое нормальное распределение, руководствуясь критерием правдоподобия
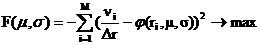
где ri – отвечающее i-му столбцу гистограммы расчетное значение доходности,
Dr – уровень дискретизации гистограммы.
Задача (5.3) – это задача нелинейной оптимизации, которое имеет решение
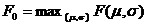
причем m0, s0 – аргументы максимума F(m,s), представляющие собой контрольную точку.
