Для этого построим частную производную цены по показателю внутренней нормы доходности бумаги:
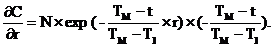
Видно, что чувствительность цены к колебаниям процентной ставки имеет нестационарный вид и убывает до нуля по мере приближения срока погашения бумаги.
Таким образом, резонно искать среднеквадратичное отклонение (СКО) шума как функцию вида:
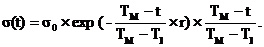
Ожидаемый вид СКО представлен на рис. 6.2.
С практической точки зрения это означает следующее. Мы наблюдаем случайный процесс цен на бумаги, который можно обозначить H(t).
Тогда шум процесса имеет вид
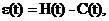
где C(t) – тренд цены - определяется по (6.6).
