Пусть бумага данного вида эмиттирована в момент времени TI по цене N0 < N, где N – номинал ценной бумаги.
Тогда разница N – N0 составляет дисконт по бумаге. Параметрами выпуска также определен срок погашения бумаги TM, когда владельцу бумаги возмещается ее номинал в денежном выражении.
Пусть t – момент времени, когда инвестор собирается приобрести бумагу.
Определим ее справедливую рыночную цену С(t).
Это выражение и является трендом для случайного процесса цены бумаги.
Пусть время в модели дискретно, а интервал дискретизации - год. Бумага выпускается в обращение в начале первого года, а гасится в конце n – го. Тогда рыночная цена дисконтного инструмента, приобретаемого в начале (k+1) – го года обращения бумаги, имеет вид:
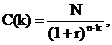
где r – внутренняя норма доходности долгового инструмента, определяемая по формуле:
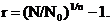
Формула (6.1) предполагает, что на рынке имеются бумаги с той же самой внутренней нормой доходности, что и наша, которые при этом имеют реинвестируемые купонные платежи, а период реинвестирования равен одному году. Если бы не так, то расчет следовало бы вести по формуле, предполагающей, что период реинвестирования платежей совпадает с периодом обращения дисконтного инструмента.
Получим аналоги формул (6.1) и (6.2) для непрерывного времени, предполагая по ходу, что реинвестирование также идет в непрерывном времени с периодом бесконечно малой длительности. Это делается следующим образом.
