Рыночное равновесие


Теперь можно поговорить о рыночном равновесии. В чем проблема равновесия?
Прежде робинзонов было двое, и каждый обладал запасом товаров. Было две функции спроса и две функции предложения. Тогда цена равновесия зависела только от соотношения интенсивности их потребностей в товаре своем и чужом.

Эта равновесная цена, как почти выяснил сам Тюрго, устанавливалась на уровне равенства предельных полезностей одного и другого товара.
Теперь ситуация стала иной.
Во-первых, их уже трое. Что качественно нового вносит такое изменение в количестве? Спрос дровосека на кукурузу зависит теперь не только от его предельной потребности в зерне, но и от его же спроса на виски. Если он готов часть своих дров обменять на веселящий напиток, значит, к обмену на маис будет предназначаться уже меньше дров, чем раньше. Отсюда меняется степень убывания полезности каждой охапки его дров.

Но ведь то же самое можно сказать и про кукурузника, и про винокура.
Мы имеем три вида сделок по обмену:
1) маис на дрова;
2) маис на виски;
3) дрова на виски.
У каждого из участников своя функция спроса на оба товара его партнеров и своя функция предложения своего товара. Таким образом, теперь мы имеем шесть функций спроса и три функции предложения. И каждая из них зависит от всех остальных.
Во-вторых, теперь в расчет берутся ресурсы производства труд и земля. Возможно такое рассуждение: если за 20 мер маиса земледелец получает кружку виски, то, чем больше маиса он произведет, тем больше кружек виски получит. И вот он начнет расширять посевную площадь и соберет значительный урожай, и окажется, что его продукт от этого просто подешевел и теперь за кружку виски ему приходится отдавать 25 мер зерна.

То же самое может произойти и с дровосеком, и с винокуром, хотя у них наращивание продукта потребует увеличения скорее затрат труда, чем площади обработки земли.
Что же делать? Сокращать производство, чтобы единица продукта стала дороже? Но можно насокращать до такой степени, что не обеспечишь себя всем необходимым.

Значит, требуется найти некое равновесное количество продукта, при котором предельный расход ресурсов будет равен предельному доходу от продажи продукта.
Но и это еще не все. Хитрый новичок может задумать комбинацию: наменяю, мол, побольше маиса, сделаю запас, потом какое-то время смогу получать дрова за маис, у кукурузника вообще ничего не покупать и устрою себе безделье. Такой поворот вносит в ситуацию элемент конкуренции: дровосек может выбирать, у кого покупать зерно в обмен на свои дрова.

Правда, для этого винокуру пришлось бы затратить предварительно много труда.
Однако земледелец, видя, что винокур покупает у него больше, чем ему нужно для собственного потребления, начинает припрятывать свой запас, повышая зерновую цену одной кружки виски. И выходит, что винокур лишь удешевил свой продукт и перерасходовал труд.
Мы видим, что даже в такой простой экономике становится очень непросто установить цены и производство на уровне равновесия. И что даже при достижении равновесия здесь могут происходить разнообразные колебания с отклонениями и возмущениями. А каким образом это все происходит в современной стране с многомиллионным населением?
Так ставил задачу Вальрас.




Постановка задач.
Начнем по порядку. Дано:

Товары
 Ресурсы
Кукуруза (К)
Земля (3)
Дрова (Д)
Труд (Т)
Виски (В)


Требуется определить: при каких ценах будет достигнуто равновесие спроса и предложения по всем трем товарам и какое количество каждого товара отвечает состоянию равновесия?
Важное уточнение: мы должны принимать во внимание, что и ресурсы производства имеют свою цену, которая влияет на цены товаров. Когда речь идет о настоящей экономике, цена земли выражается рентой, а цена труда заработной платой. В нашей ситуации нет ни дворянина-землевладельца, ни наемного труда.

Но от Адама Смита и Иоганна фон Тюнена мы уже знаем, что и рента, и зарплата на острове Тюрго тоже будут существовать, хотя и в скрытом виде. Так что островная наша экономика в этом отношении не отличается от обычной;
Настала пора ввести некоторые обозначения:
а расход любого ресурса на создание единицы любого продукта;


aij расход ресурса i на создание единицы продукта j, например: аЗК расход земли на выращивание одной меры кукурузы, aTB расход труда на изготовление одной кружки виски и т.д. Такой показатель имеет название технологического коэффициента;
xi количество единиц продукта i (те. сколько его производится для обмена);
ri количество единиц ресурса ; (т.е.. сколько его всего используется в производстве всех продуктов);
pi цена единицы продукта i;
vi цена единицы ресурса i.
Может возникнуть вопрос чем измеряются цены в этой бартерной экономике? Островитяне наши долго ломали голову, пока не придумали измерять „цены трудоднями”1. Они договорились считать 8 часов труда за 1 трудодень независимо от того, сколько в действительности каждый из них трудится.

Уравнения общего равновесия.

Немного поразмыслив, мы можем записать основные зависимости нашей островной экономики в виде уравнений.
Возьмем сперва ограничения по ресурсам. Очевидно, что количество каждого ресурса, которое используется в производстве кукурузы, дров и виски, не может не быть равно в сумме тому количеству этого ресурса, каким располагает наше хозяйство. Поэтому:

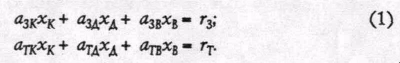
Сейчас возьмемся за цены. Всего их у нас 5 (цены трех продуктов + цены двух ресурсов). Цены служат аргументами функций спроса. Мы здесь имеем дело не с обычной кривой спроса, потому что мы теперь знаем, что спрос на каждый отдельный товар зависит (так или иначе) от цен на все товары и ресурсы в экономике.

Как зависит? Пока это неважно, потому что мы пока не собираемся заниматься вычислениями. Поэтому мы просто констатируем, что спрос на данный товар есть какая-то функция от всех цен (функция типа F). И потому мы можем записать систему из трех уравнений спроса (по трем продуктам):

(2)

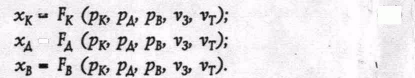
Далее, мы вспоминаем, что цена товара равна сумме издержек его производства. Нам известны технологические коэффициенты (которые показывают, сколько каждого ресурса используется на отдельный продукт). Умножая технологические коэффициенты на цены ресурсов, получаем сумму издержек производства по каждому продукту:
aЗКvЗ+aTKvT=pK (3)
aЗДvЗ+aТДvT=pД
аЗBvЗ+aTBvT=pB

Нам осталось записать функции предложения ресурсов (факторов) производства. Как и с функциями спроса на товары, мы запишем их в общем виде просто функции типа G:
(4)
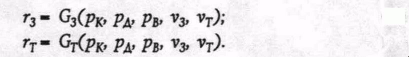
Это еще не все. Пока даже непонятно, к чему все эти уравнения, правда ведь? Ну что же, давайте прибегнем к испытанному методу.

Что нужно делать, если хочешь что-то понять? Конечно: рассуждать.



Закон Вальраса
Доход земледельца проистекает от его земли и его труда, а выражается в выручке от продажи кукурузы. Иными словами, выручка от продажи кукурузы распределяется как рента на его землю и оплата его труда (это и есть то, что мы называли прежде вознаграждением факторов производства). То же самое можно сказать про двоих других островитян, не так ли?

А если так, тогда внимание! вся суммарная выручка от продажи всех (трех) продуктов является суммой вознаграждений всех (двух) факторов, используемых на острове. И вот что получается:
рКхК+рДхД+зВхВ=vЗrЗ+vТrТ (5)
Знак тождества мы ставим здесь потому, что левая часть и правая часть, как мы только что установили, это одно и то же. Но и тут еще не конец. Мы только что понаписали кучу уравнений.

В ней есть уравнения спроса (в левой части стоят иксы) и уравнения предложения (в левой части стоят эры). Вот давайте-ка их быстренько подставим из уравнений (2) и (4) в тождество (5):
PKFK+pДFД+pBFB=v3G3+vTGT (6)
Вот теперь все. Во-первых, мы пишем просто буквы F и G, помня, что это функции спроса и предложения. А во-вторых
О, тут стоит сделать паузу. В общем, выражение (6) есть не что иное, как знаменитый Закон Вальраса.

Значение закона Вальраса и что он дает.

Сперва укажем, для чего Закон Вальраса не применяется. Он не используется для вычисления цен и других показателей Нужен Закон Вальраса для рассуждении. О чем говорит этот закон?

Он говорит о том, что в состоянии рыночного равновесия совокупный спрос равен совокупному предложению. Но это звучит чересчур общо. Вернемся к тождеству (5).

О чем оно нам говорит? О том, что совокупные доходы равны совокупным расходам. Сказать (5) значит сказать (6).

И наоборот.
Словесная формулировка выражения (5) напоминает что-то такое, что мы давно уже проходили. Ну конечно, все уже догадались: тождество Сэя!
Действительно, Закон Вальраса сильно напоминает Закон Сэя в варианте "тождества". Можно сказать больше: если брать Закон Вальраса в том виде, как мы его подали выше, он просто идентичен тождеству Сэя.
Однако сам Вальрас, понятное дело, имел в виду не остров с тремя производителями, а народное хозяйство современной страны, где многие тысячи производителей поставляют на рынок сотни тысяч видов товаров, покупаемых миллионами потребителей. Так что Закон Вальраса нужно записать в более общем виде:
сумма всех pjFj = сумме всех viGi
Мы уже раньше условились о том, что ресурс i это любой ресурс.



Содержание раздела