Уравнения движения в энергетическом представлении
2.3 Уравнения движения в энергетическом представлении
Попытаемся теперь на конкретном примере продемонстрировать какую дополнительную научную информацию мы можем получить, используя предложенный подход.
Рассмотрим уравнение движения для произвольного объекта. Его легко получить на основе упомянутого выше лагранжева формализма, используя наиболее общий подход, который применяется при выводе тензора энергии-импульса произвольной системы [38].
Напомню, что уравнение движения получают согласно принципу наименьшего действия путем варьирования D, и оно имеет вид [38]
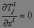
(1)
Равенство нулю дивергенции (1), означает, что сохраняется интеграл от тензора по гиперповерхности пространства. Этот тензор Т с компонентами Tjl (j,l = 0,1,2,3) называется тензором энергии-импульса системы. Он определен неоднозначно, а только с точностью до градиента произвольного антисимметричного тензора. Для его однозначного определения можно потребовать, чтобы существовала принятая в механике связь между импульсом и моментом импульса.
В этом случае получаем дополнительное условие Tjl=Tlj, т.е. тензор энергии-импульса должен быть симметричен.
Как известно [38], компонента T00 этого тензора характеризует плотность энергии. Вектор с компонентами T10/c, T20/c, T30/c есть плотностью импульса, а вектор с составляющими cT01, cT02, cT03 – плотность потока энергии – количество энергии, протекающей в единицу времени через единицу поверхности. Ввиду симметричности тензора, мы имеем связь между потоком энергии и импульсом: плотность потока энергии равна плотности импульса, умноженной на c2. Компоненты Tik (i, k =1, 2, 3) составляют трехмерный тензор плотности потока импульса.
Взятые со знаком минус они образуют тензор напряжений. Плотность потока энергии есть вектор; плотность же потока импульса, который сам по себе вектор, должна быть тензором второго ранга.
Делается вывод [38], что скорость изменения энергии, находящейся в объеме V равна количеству энергии, протекающей через границу этого объема в единицу времени, и скорость изменения импульса системы в объеме V есть количество импульса, вытекающее в единицу времени из этого объема (см. уравнения (4), (5) чуть ниже).
На этом обычно заканчивается анализ уравнений движения произвольной системы, и далее используют различные приближения, чтобы упростить общий вид тензора энергии- импульса в конкретных частных задачах.
Однако уже в общем случае тензора энергии- импульса произвольной системы, нас не устраивает та часть интерпретации уравнений движения, в которой используется импульсное представление. Оно более подходит для описания локальных объектов, а в нашем случае непрерывных полевых структур предпочтительно использовать энергетическое представление. Поэтому сейчас мы постараемся от импульсной интерпретации перейти к энергетической и проанализируем уравнения движения уже в этих терминах.
Рассмотрим эти хорошо известные уравнения. Они получаются из (1) разделением на пространственные и временные производные [38]:
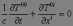
(2)

(3)
Эти уравнения затем интегрируются по некоторому произвольному объему пространства V, и применяется теорема Гаусса.
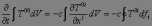
(4)
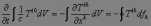
(5)
где интеграл справа берется по поверхности, охватывающей объем V (df1, df2, df3 – компоненты трехмерного вектора элемента поверхности df).
Рассмотрим второе уравнение (5). Поскольку результаты, полученные при анализе этого уравнения, будут широко использоваться в дальнейшем, остановимся на нем более подробно.
Левая часть не вызывает вопросов, здесь стоит скорость изменения импульса в объеме V, т.е. сила, действующая на этот объем. А вот в правой части перейдем к энергетическому представлению и для этого воспользуемся аппаратом дифференциальной геометрии, теоретические основы которого можно почерпнуть из [41], а достаточно подробное применение этих методов в физике и, в частности к тензору энергии- импульса, хорошо изложено в [42].
Очень кратко напомним смысл основных понятий дифференциальной геометрии, которыми нам придется оперировать. Прежде всего, это касается еще одного геометрического объекта – “дифференциальная форма”, который, наряду с другими хорошо известными геометрическими объектами (скаляр, вектор, тензор), описывает физические величины. В частности, более подробно рассмотрим понятие 1-формы.
Может возникнуть закономерный вопрос, зачем вообще нужны дифференциальные формы, и нельзя ли обойтись хорошо известными старыми понятиями? Чтобы ответить на этот вопрос можно привести следующий пример [42].
Рассмотрим привычное определение вектора 4-импульса p для частицы, например электрона, с массой m и вектором 4-скорости u, т.е. p=mu. Кроме этого, в физике известен и другой подход к понятию импульса, при котором каждой частице приписывается волна деБройля. Эта волна имеет самый непосредственный физический смысл, ее дифракция на кристаллической решетке позволяет определить не только длину волны, но и ту конфигурацию в пространстве, которую образуют поверхности равных целочисленных значений фазы.
Конфигурация этих поверхностей дает простейшую иллюстрацию, которую удается нHйти для 1-формы. Определив эти поверхности посредством выражения ћ?фаза, мы получим “1-форму импульса” p .
Посмотрим, что может нам дать такое представление импульса. Возьмем произвольный 4-вектор v. Он пересечет определенное число поверхностей целой фазы. Обозначим это число пересечений посредством выражения p ,v. Как правило, начало и конец вектора v не лежат на поверхностях целочисленных фаз.
Чтобы определить более точное значение числа пересечений (перейти от целого числа к вещественному), необходимо в этих позициях между соседними поверхностями целой фазы распределить бесконечное число поверхностей со всеми промежуточными значениями фазы. Далее, чтобы понятие 1-формы стало рабочим инструментом, нужно сделать еще один небольшой шаг. Необходимо трактовать 1-форму не как глобальную конфигурацию поверхностей уровня, а как некоторую аппроксимацию этих поверхностей в элементарном, бесконечно малом объеме в виде плоских поверхностей, расположенных на равных расстояниях друг от друга (линейное приближение).
Плоские поверхности 1-формы в этом малом объеме дадут наилучшую линейную аппроксимацию искривленных поверхностей уровня, а сама 1-форма становится линейной функцией, и появляется возможность оперировать ей, как и любой другой функцией. Нетрудно убедиться, что совокупность всех 1-форм в данном событии (4-точке) образует векторное пространство в абстрактном, алгебраическом смысле этого понятия. Существует и взаимно однозначное соответствие между произвольным вектором n, и соответствующей ему 1-формой n в виде n ,v=nv, т.е. число пересеченных поверхностей произвольным вектором v у некоторой 1-формы n , равно проекции вектора v на вектор n (точка обозначает скалярное произведение).
Таким образом, дифференциальная геометрия дает исследователю надежный математический формализм, позволяющий установить взаимно однозначное соответствие между локальным точечным описанием физических величин (импульс в данной точке в виде вектора) и нелокальным описанием (тот же импульс, но уже в объеме, окружающем эту точку в виде 1-формы). А значит, учитывая наши цели, необходимо поближе познакомиться с этим геометрическим объектом (небольшое дополнение см. в Приложении А).
Нам понадобится еще одно понятие дифференциальной геометрии. Это 1-форма объема. Достаточно будет ограничиться частным случаем этого понятия для трехмерного куба в системе отсчета, относительно которой он находится в покое. В этом случае 1-форма объема с 4-скоростью u и ребром L определяется [42] как = –Vu = L3dt в случае стандартной положительной ориентации u в прошлое (u=–dt), или в другом варианте =L2tdx.
По своему геометрическому смыслу 1-форма объема представляет собой объем “заметаемый” со временем, либо за счет движения самого объема (первый вариант), либо за счет движения одной из его граней, например, площадки Syz=L2 в направлении x со скоростью u (второй вариант).
1-форма произвольного объема может быть проанализирована путем разбиения ее на введенные элементарные объемы.
Теперь мы имеем уже все необходимые понятия, чтобы сформулировать определение тензора энергии-импульса в терминах дифференциальных форм [42]: тензором энергии-импульса называется линейный оператор с двумя входными каналами, в один из которых вводится 1-форма объема , а в другой произвольный вектор w или 1-форма , и в результате получается проекция 4-импульса на этот вектор или 1-форму соответственно, т.е.
T(w, )=wp, T(, )=,p. (6)
Это определение позволяет легко получить компоненты тензора энергии импульса в чисто энергетическом представлении, поскольку проекция импульса p на 4-вектор скорости наблюдателя u, дает энергию, измеренную наблюдателем, взятую с обратным знаком, т.е. E= –up [42].
Пространственные компоненты Tik из (5) можно интерпретировать, если рассмотреть двумерную грань 1-формы объема, положительная нормаль к которой направлена по k. За время t эта поверхность заметает 3-объем 1-форма которого равна = L2k tdxk. Поместим наблюдателя на эту поверхность. В отличие от общепринятого подхода, когда наблюдатель неподвижно сидит на поверхности и измеряет проекции импульса, пересекающего площадку на направления единичных векторов в своей лоренцевой системе [42], мы заставим наблюдателя двигаться с некоторой скоростью u поочередно вдоль всех своих координатных осей. За время t он сканирует всю площадку, и прилегающий объем, отмечая происходящие изменения. Проецируя 4-импульс p, пересекающий поверхность, на свою скорость, наблюдатель получает информацию о распределении энергии в различных направлениях.
На первый взгляд может показаться, что такой подход не имеет смысла, поскольку численное значение энергии, полученное наблюдателем, зависит от его собственной скорости, и результат измерения будет неоднозначным. Однако, как будет показано ниже, существует энергетическая характеристика, независящая от скорости наблюдателя и имеющая однозначный физический смысл.
- Несколько слов о гравитации
- Основное следствие
- Физическая модель
- Практическая реализация запутанных состояний сознания
- Приложение а
