ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Рис. 23
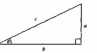
Прежде чем мы перейдем к мандале, я хотел бы ввести новую тему, поскольку есть еще один вопрос, который окажется для нас важным. Нам опять предстоит заняться математикой и ознакомиться с очередной игрушкой. Есть несколько тригонометрических функций (см. рис. 23) — синус, косинус, тангенс, котангенс и так далее, — но мы поговорим только об одной из них: о синусе. Мы произносим это название как синус, но обычно эту функцию записывают в сокращенной форме: sin.
Синус угла равен а/с, косинус — b/с, тангенс — а/b, а котангенс — b/а, но мы не будем рассматривать остальные функции. Я хочу построить одну кривую. Давайте начертим такую окружность (см. рис. 24):
ПОСТРОЕНИЕ СИНУСОИДЫ
Рис. 24
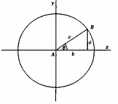
Вновь скажем: Будем считать это окружностью, хотя эта кривая получилась совсем не круглой. Будем считать расстояние между точками А и В равным 1. Все углы будем измерять в радианах, то есть в отношениях радиуса окружности к ее длине. Полная длина окружности составляет ровно пи радиан. Поскольку длина данного отрезка равна единице, то синус, который определяется как а/с, становится равным а/1, то есть просто а, что облегчит наши рассуждения. По мере того как отрезок АВ вращается против часовой стрелки вокруг своего начала в точке А, точка меняет свое положение, а длина а увеличивается.
Наконец, когда отрезок АВ достигает вертикального положения, а становится равным 1. Существует соглашение о том, что направления вверх и вправо являются положительными, а влево и вниз — отрицательными. Орезок продолжает вращаться, а значение синуса увеличивается, затем вновь уменьшается вплоть до нуля (когда АВ накладывается на ось X), далее становится отрицательным и достигает -1 (когда вращающийся отрезок совпадает с нижней полуосью У), потом снова увеличивается до нуля (когда отрезок совмещается с правой полуосью X) и возвращается к исходному значению. Представим себе, что такое вращение продолжается вечно, и начертим соответствующую кривую (см. рис. 25),
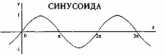
Рис. 25
которая представляет последовательность полученных таким способом значений синуса. Эта кривая может представлять все другие кривые, для чего и используется во многих приложениях. Некоторые отметят, что эта кривая соответствует второму основополагающему принципу Тайной доктрины:
Вторым утверждением Тайной доктрины является полная всеобщность того закона периодичности, приливов и отливов, подъемов и спадов, который наблюдается и отмечается физическими науками во всех отделах природы. Такие чередующиеся явления, как День и Ночь, Жизнь и Смерть, Сон и Бодрствование, представляют собой факты настолько распространенные, всеобщие и не знающие исключения, что очень легко понять: перед нами один из самых основополагающих Законов Мироздания [4].
Введем обозначения длины по осям координат X и У. Легко убедиться, что, когда угол равен нулю, синус также равен нулю. После этого синусоида поднимается от центра координат, достигает в своей высшей точке значения 1, вновь опускается к оси X, когда угол равняется 180, то есть пи радиан. Кривая продолжает опускаться ниже оси X, а потом снова пересекается с ней в точке 2 . Этот участок кривой соответствует обороту на 360, или 2 , но, поскольку наш отрезок, как стрелка, вращается бесконечно, кривая не обрывается.
Она уходит в безграничное прошлое и в бескрайнее будущее, у нее нет конца. Вообще говоря, эту кривую используют для представления множества периодичных процессов, но я намерен применить ее лишь к одному явлению — жизни. Вот точка рождения, точка смерти, точка нового рождения и так далее.
Мы ограничимся, впрочем, только психическим рождением и психическим исчезновением.
Не будем обращать внимания на физическое тело. Это только досадная помеха. В связи с этим я хочу выразить большую симпатию к воззрениям Плотина — он стыдился того, что у него есть физическое тело, — и Шанкары, который придерживался строгой вайрагьи.
Шанкара говорил: Что такое тело? Это просто мешок. Он сделан из кожи, костей, сухожилий и наполнен навозом, мочой и слизью. Как можно питать к нему привязанность?
Думаю, современные анатомы и физиологи сочли бы такое описание слишком кратким, но общий смысл вполне понятен. Шанкара хотел вызвать у себя вайрагью. Слово вайрагъя означает отвращение. Если вы испытываете отвращение к миру внешних, явственных форм и устремление к миру высшему, то извлекаете пользу и от толчка снизу, и от рывка сверху; это очень помогает — стремление тянет ввысь, а вайрагья отталкивает от низшего.
Вот в этом и суть: мы будем полностью игнорировать физическое.
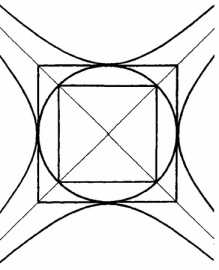
Рис. 26
Нас интересует психическое. Здесь сознание возвышается (этот подъем олицетворяется восхождением кривой над начальной точкой); сознание нацелено на окружающий мир, каким мы его знаем, а позади него, ниже него простирается огромное царство под названием Бессознательное; оно несомненно воздействует на нас, обращается к нам посредством сновидений, гипногогических видений и другими, менее ощутимыми способами, никогда не выдвигаясь при этом на первый план сознания. Так называемая точка смерти (то место, где кривая, опускаясь, пересекается с прямой) представляет собой просто момент обращения: в этот миг то, что размещалось на переднем плане сознания, отступает в тень, а прежнее бессознательное или некая его часть выступает вперед.
Мы переживали это уже стократно, тысячекратно, но обычно человек несколько устает от того, что повторяется гуголы раз. У него возникает желание понять, как разорвать этот замкнутый круг, ведь в нем нет никакого развития, только непрекращающееся движение от безграничного прошлого к столь же бескрайнему будущему, вновь и вновь, круг за кругом. Хочется вырваться. И вот здесь возникает мандала (см. рис. 26).
Ее нарисовал для меня один из помощников, профессиональный чертежник. Исходная кривая была представлена на рисунке 21 (теперь она повернута на /4 радиан). Очевидно, требовалась симметрия, и это привело к использованию так называемой сопряженной гиперболы; затем был добавлен квадрат, стороны которого касаются ветвей гиперболы в ее вершинах.
Потом в этот квадрат была вписана окружность, в нее — еще один квадрат, после чего я почувствовал себя вполне удовлетворенным. Именно так разрастается мандала. Вы можете убедиться в том, что этот чертеж соответствует условиям построения мандалы, то есть требованиям четырехсторонней и круговой симметрии. Однако, как правило, мандала становится эстетическим произведением, ее пишут как картину, и даже, по словам Юнга, танцуют, но в данном случае это не эстетическое, а концептуальное построение. Рисунок только указывает на некий принцип, и такой факт делает его нетипичным: это умозрительная, теоретическая мандала, а не эстетическое творение.
И все же ее разрастание на протяжении долгих лет вплоть до того момента, когда я испытал удовлегворение, может служить типичным примером подобного процесса. Он олицетворяет образование некоторой целостности. Юнг говорит, что мандала обычно означает возникновение Я в процессе преображения личности.
Какие бы трудности ни ждали человека впереди, в тот миг, когда пациент выплескивает из себя мандалу, она оказывает на него целительное воздействие.
Теперь мне хочется, чтобы вы обратили внимание на взаимоотношения внутреннего квадрата и круга. Этот вписанный квадрат является прообразом полной определенности, достигаемой с помощью конечного набора характеристик, окончательно и полно определенных понятий, точного измерения; круг олицетворяет то же самое, что и в Великой Пирамиде, да и во всей символике вообще: нечто кроющееся за рамками любых определимых понятий, древний Мир Небесный, сферу непостижимого. Однако круг вписан в квадрат, означающий, что мы достигли в своем развитии уровня утонченных понятий, того типа определимых -неопределимых концепций, который позволяет мыслить о прежде немыслимом. В свою очередь, эта область ограничивается уже не кругом, а симметричной гиперболой, которая уходит в беспредельность и, следовательно, охватывает собой бесконечную площадь — в отличие от окружности, вмещающей лишь ограниченное пространство.
Мы вновь направляемся к безграничным бесконечностям, к нехоженым бескрайним бесконечностям Запредельного. У окружности есть тригонометрические функции, порождающие кривую, которая просто тянется бесконечно; подобно этому, существуют гиперболические функции — они порождаются равносторонней гиперболой и имеют совершенно иной вид. Соответствующие этим функциям кривые возрастают неограниченно, они лишены периодичности, это только восхождение или нисхождение. Но когда речь идет о пространстве и сознании, подъем и падение получают одинаковое содержание.
Мы вырвались из замкнутого круга, и потому здесь символически отражен смысл Освобождения. Это служит дополнением к тому, что я говорил в прошлый раз о неопределимом, теоретическом непрерывном пространстве, о пребывающей в процессе становления йоге Запада — не о прежних ее формах, принадлежащих другим народам, иным нравам, а о том, что присуще западному человеку, опирающемуся на теории.
- Математика, философия и йога
- Лекция 2 НЕДВОЙСТВЕННОЕ СОЗНАНИЕ
- Заботиться о них - мой долг.
- Концепции, входящие в шастры и сутры
- Лекция 3 Что такое раджа-йога
