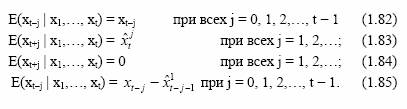|
|

|
|
|
Правые части этих соотношений представляют собой линейные комбинации p + k предшествующих (по отношению к левой части) значений анализируемого процесса xτ, дополненные линейными комбинациями текущего и q предшествующих значений случайных остатков δτ. Причем коэффициенты, с помощью которых эти линей- ные комбинации подсчитываются, известны, т.к. выражаются в тер- минах уже оцененных параметров модели. Этот факт и дает возможность использовать соотношения (1.81) для построения прогнозных значений анализируемого временного ряда на l тактов времени вперед. Теоретическую базу такого подхода к прогнозированию обеспечивает известный результат, в соответствии с которым наилучшим (в смысле среднеквадратической ошибки) линейным прогнозом в момент времени t с упреждением l является условное математическое ожидание случайной величины xt+l, вычисленное при условии, что все значения xτ до момента времени t. Этот результат является частным случаем общей теории прогнозирования (см. [237, 198, 235]). Условное математическое ожидание
получается применением операции усреднения к обеим частям (10) при τ = t + l с учетом следующих соотношений:
Таким образом, определяется следующая процедура построения прогноза по известной до момента траектории временного ряда: по формулам (1.81) вычисляются ретроспективные прогнозы 1 1 ˆ t − x по предыдущим значениям временного ряда; при этом при вычислении начальных прогнозных значений 1 ˆ t −q+m− x для xt−q+m (m = 0, 1,…) по формулам (1.81) вместо условных средних E(δt−q+m−j | x1,…, xt−q+m), которые в общем случае следовало бы вычислять по формулам (1.85), подставляются их безусловные значения, равные нулю; используя формулы для τ > t и правила (1.82)−(1.85) подсчи- тываются условные математические ожидания для вычисления про- гнозных значений. Описанная процедура выглядит достаточно сложной. Однако при реалистичных значениях параметров p, q и k эта процедура в действительности оказывается весьма простой. 1. В чем состоят основные отличия стационарных временных рядов от нестационарных? 2. В чем состоит идентификация моделей ARIMA? 3. Какова последовательность процесса идентификации моделей прогнозирования, содержащих сезонную компоненту? 4. Каков алгоритм (процедура) построения прогнозов на базе модели ARIMA? |
Прогнозирование на базе ARIMA-моделей 2 |